May 8, 2019
Introduction
From Wikipedia:
Word embedding is the collective name for a set of language modeling and feature learning techniques in natural language processing (NLP) where words or phrases from the vocabulary are mapped to vectors of real numbers. Conceptually it involves a mathematical embedding from a space with many dimensions per word to a continuous vector space with a much lower dimension.
The main function is to create a vector of numbers that represent a word based on the context in which that word is used. These vectors can then be used in a relative fashion to determine the relatedness of words.
Notebook Links
View the IPython notebook for this session on Github here
Or launch the notebook in Google Colab or MyBinder:
Papers
Here is a list of the seminal papers that led to the capability available today for word and document vectors:
- 2013 – Distributed Representations of Words and Phrases and their Compositionality Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, Jeffrey Dean – https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf
- 2013 – Efficient Estimation of Word Representations in Vector Space Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean – https://arxiv.org/pdf/1301.3781.pdf
- 2014 – Distributed Representations of Sentences and DocumentsQuoc V. Le, Tomas Mikolov – https://arxiv.org/pdf/1405.4053
- 2015 – From Word Embeddings To Document Distances Matt J. Kusner, Yu Sun, Nicholas I. Kolkin, Kilian Q. Weinberger – http://proceedings.mlr.press/v37/kusnerb15.pdf
Word Vectors
In order to compute the word vectors, we create a neural network and train it to predict things based on either a Skip-gram or Continuous Bag of Words approach. The weights of the hidden layer then become the values used in the word vector.
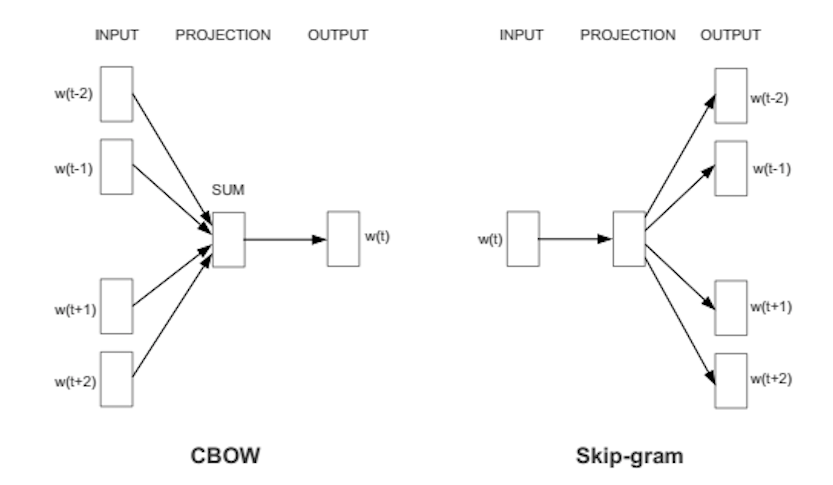
Image from Efficient Estimation of Word Representations in Vector Space

Image from StitchFix Blog
Document Vectors
Document Vectors are created by adding an additional document (or paragraph) ID as an input.
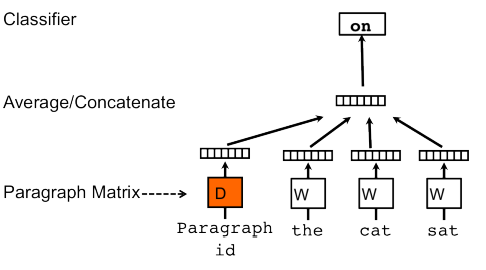
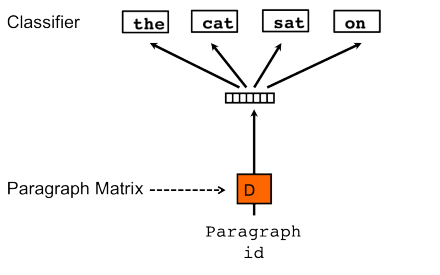
Images from A gentle introduction to Doc2Vec
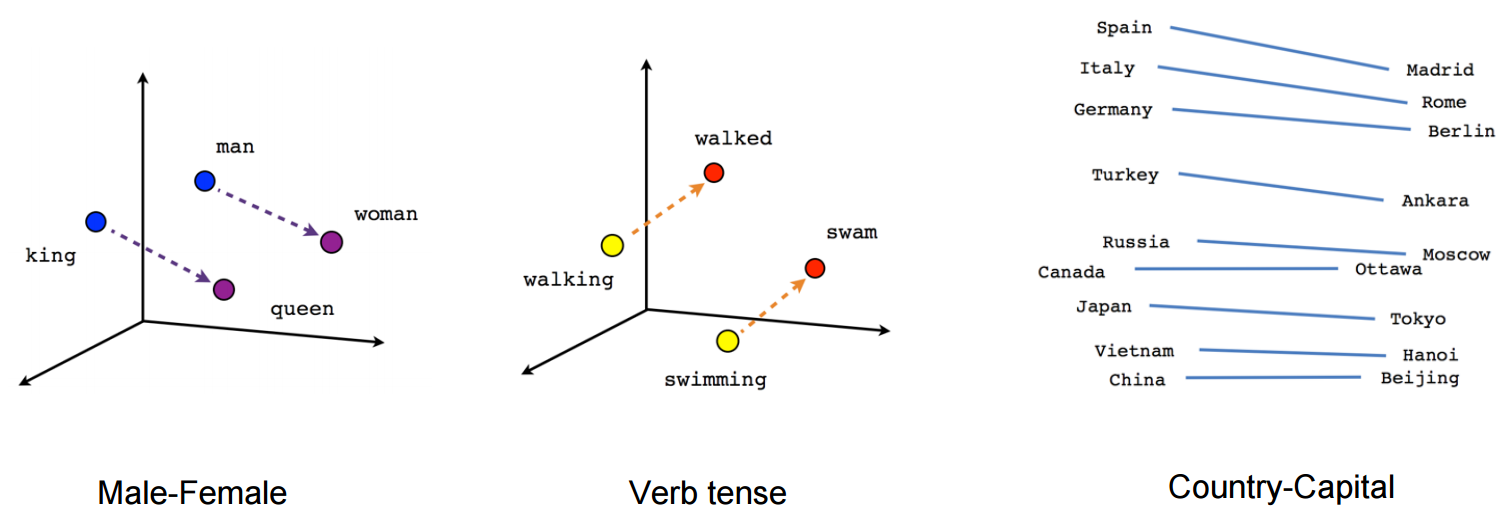
Image from Vector Representations of Words

Image from Introduction to Word Embedding and Word2Vec
Word Movers Distance
The distance between words of different sentences can be used to judge the similarity of the sentences or documents.
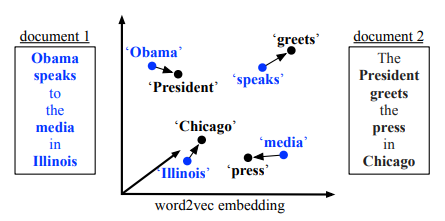
Image from From Word Embeddings To Document Distances
References
Application
Below, we will walk through some examples from the Fast.ai Word Embeddings Workshop.
#Get the data and untar it
!wget http://files.fast.ai/models/glove_50_glove_100.tgz
!tar xvzf glove_50_glove_100.tgz
--2019-05-08 18:34:26-- http://files.fast.ai/models/glove_50_glove_100.tgz
Resolving files.fast.ai (files.fast.ai)... 67.205.15.147
Connecting to files.fast.ai (files.fast.ai)|67.205.15.147|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 225083583 (215M) [text/plain]
Saving to: ‘glove_50_glove_100.tgz.1’
glove_50_glove_100. 100%[===================>] 214.66M 107MB/s in 2.0s
2019-05-08 18:34:28 (107 MB/s) - ‘glove_50_glove_100.tgz.1’ saved [225083583/225083583]
glove_vectors_100d.npy
glove_vectors_50d.npy
words.txt
wordsidx.txt
#import packages needed
import pickle
import numpy as np
import re
import json
np.set_printoptions(precision=4, suppress=True)
We will load the glove 50 & 100 vectors as numpy arrays and load the words and word indices as arrays.
vecs = np.load("glove_vectors_100d.npy")
vecs50 = np.load("glove_vectors_50d.npy")
with open('words.txt') as f:
content = f.readlines()
words = [x.strip() for x in content]
wordidx = json.load(open('wordsidx.txt'))
Now let’s see what this data looks like…
len(words)
400000
words[:10]
['the', ',', '.', 'of', 'to', 'and', 'in', 'a', '"', "'s"]
wordidx['architect']
4493
words[4493]
'architect'
What about that word vector?
vecs[4493]
array([-0.2675, -0.1654, -0.6296, 0.448 , 0.452 , -0.6424, 0.042 ,
-1.0137, -0.6596, 0.9818, 0.2998, -0.7044, 0.0481, -0.3909,
-0.2515, -0.0907, 0.5111, 0.2321, -1.3972, 0.0896, -1.0962,
0.1159, 0.0979, -0.7837, 0.1524, -1.3648, -0.5557, -1.0818,
-0.2341, -0.6261, -0.8803, 0.536 , 0.1439, 0.335 , -0.4361,
-0.0788, 0.2288, -0.4465, 0.6148, -0.2139, 0.4312, 0.1618,
1.0763, 0.4359, 0.4286, -0.3155, -0.0784, -0.5784, -0.1905,
0.1904, -0.1977, -0.5946, 0.6593, 0.2798, -0.0671, -1.6904,
-0.9657, 0.044 , 0.3146, -0.491 , 0.3345, 0.3266, 0.3003,
0.4409, 0.7353, -0.599 , 0.1626, 1.012 , -0.3043, -0.1179,
-0.3546, 0.6402, -0.8409, -0.3581, 0.1925, -1.1535, 0.6362,
0.8889, -0.0116, -0.2549, 0.3039, 0.2562, -0.0331, 0.4997,
-0.0159, 0.3529, -0.2008, -0.5076, -0.4175, -1.4415, 0.7295,
-0.8933, 0.5672, 0.607 , 0.0374, 0.0441, -0.2491, -1.014 ,
0.0384, -0.5015], dtype=float32)
from scipy.spatial.distance import cosine as dist
Smaller numbers mean two words are closer together, larger numbers mean they are further apart.
The distance between similar words is low:
dist(vecs[wordidx["puppy"]], vecs[wordidx["dog"]])
0.27636247873306274
And the distance between unrelated words is high:
dist(vecs[wordidx["avalanche"]], vecs[wordidx["antique"]])
0.9621107056736946
Data Bias
The word vectors will pick up any bias that exists in the data used to build the vectors:
dist(vecs[wordidx["man"]], vecs[wordidx["genius"]])
0.5098515152931213
dist(vecs[wordidx["woman"]], vecs[wordidx["genius"]])
0.689783364534378
Nearest Neighbors
We can also see what words are close to a given word.
from sklearn.neighbors import NearestNeighbors
neigh = NearestNeighbors(n_neighbors=10, radius=0.5, metric='cosine', algorithm='brute')
neigh.fit(vecs)
distances, indices = neigh.kneighbors([vecs[wordidx["antique"]]])
[(words[int(ind)], dist) for ind, dist in zip(list(indices[0]), list(distances[0]))]
[('antique', 1.1920929e-07),
('antiques', 0.18471009),
('furniture', 0.2613591),
('jewelry', 0.26212162),
('vintage', 0.28011894),
('handmade', 0.32542467),
('furnishings', 0.3287084),
('reproductions', 0.33931458),
('decorative', 0.35905504),
('pottery', 0.3720798)]
Math with Word Vectors
You can do some pretty interesting things with these word vectors. We can combine multiple terms and use them as a single input.
new_vec = vecs[wordidx["artificial"]] + vecs[wordidx["intelligence"]]
print(new_vec)
[ 0.0345 -0.1185 0.746 0.3256 0.3256 -1.4699 -0.8715 -0.9421 0.0679
0.922 0.6811 -0.3729 1.0969 0.7196 1.3515 1.2493 0.6621 0.1901
-0.2707 -0.0444 -1.232 0.1744 0.7577 -0.9177 -1.2184 0.6959 -0.1966
-0.415 -0.3358 0.5452 0.589 -0.0299 -0.9744 -0.8937 0.2283 -0.2092
-1.3795 1.7811 0.2269 0.47 -0.3045 -0.1573 -0.478 0.3071 0.4202
-0.4434 0.1602 0.1443 -0.9528 -0.5565 0.7537 0.182 1.4008 1.8967
0.595 -3.0072 0.6811 -0.2557 2.0217 0.7825 0.4251 1.3615 0.5902
-0.1312 0.9344 -0.5377 -0.3988 -0.6415 0.6527 0.5117 0.7315 0.1396
0.3785 -0.6403 -0.094 0.1076 0.6197 0.2537 -1.4346 1.169 1.6931
0.1458 -0.5981 0.8195 -3.1903 1.2429 2.1481 1.6004 0.2014 -0.2121
0.3698 -0.001 -0.628 0.2869 0.3119 -0.1093 -0.6341 -1.7804 0.5857
0.3702]
distances, indices = neigh.kneighbors([new_vec])
[(words[int(ind)], dist) for ind, dist in zip(list(indices[0]), list(distances[0]))]
[('intelligence', 0.1883161),
('artificial', 0.25617576),
('information', 0.3256532),
('knowledge', 0.336419),
('secret', 0.36480355),
('human', 0.36726683),
('biological', 0.37090683),
('using', 0.3773631),
('scientific', 0.38513905),
('communication', 0.3869152)]
You can even move from one place to another in the vector space. Beware of bias taking you in unintended directions though. Here’s the general sense of the word “programmer”
distances, indices = neigh.kneighbors([vecs[wordidx["programmer"]]])
[(words[int(ind)], dist) for ind, dist in zip(list(indices[0]), list(distances[0]))]
[('programmer', 0.0),
('programmers', 0.32259798),
('animator', 0.36951017),
('software', 0.38250887),
('computer', 0.40600342),
('technician', 0.41406858),
('engineer', 0.4303757),
('user', 0.4356534),
('translator', 0.43721014),
('linguist', 0.44948018)]
Here’s the masculine sense of the word “programmer”
new_vec = vecs[wordidx["programmer"]] + vecs[wordidx["he"]] - vecs[wordidx["she"]]
distances, indices = neigh.kneighbors([new_vec])
[(words[int(ind)], dist) for ind, dist in zip(list(indices[0]), list(distances[0]))]
[('programmer', 0.17419636),
('programmers', 0.4133587),
('engineer', 0.46376407),
('compiler', 0.46731704),
('software', 0.4681465),
('animator', 0.4892366),
('computer', 0.5046158),
('mechanic', 0.5150067),
('setup', 0.51882535),
('developer', 0.51953185)]
Here’s the feminine sense of the word “programmer”
new_vec = vecs[wordidx["programmer"]] - vecs[wordidx["he"]] + vecs[wordidx["she"]]
distances, indices = neigh.kneighbors([new_vec])
[(words[int(ind)], dist) for ind, dist in zip(list(indices[0]), list(distances[0]))]
[('programmer', 0.19503415),
('stylist', 0.42715955),
('animator', 0.4820645),
('programmers', 0.48337305),
('choreographer', 0.4862678),
('technician', 0.4862805),
('designer', 0.48710012),
('prodigy', 0.49118334),
('lets', 0.49730027),
('screenwriter', 0.49754214)]
